Thorne Brandt

I've been studying writing glsl shaders from scratch and one of the best resources available for developing intuitive understanding is The Book of Shaders, but I've noticed that the author has left it unfinished for the better part of a decade. There doesn't seem to be much resources available online concerning the actual answers to the end-of-chapter challenges, so I felt like a lot of people were permanently left in the dark wondering whether or not they actually wrote their shaders correctly or even learned anything and eventually gave up on studying shaders. I decided I would try to blog solutions as I work through them for those stuck explorers.

There was an interesting part in the Patterns chapter of The Book of Shaders, which seemed to divide up the shader matrix into blocks with an index number and distort the effects in that block of space based on this index variable. There was this provided code that was parsed within the function with if/else blocks.

//  Give each cell an index number
//  according to its position
float index = 0.0;
index += step(1., mod(_st.x,2.0));
index += step(1., mod(_st.y,2.0))*2.0;

//      |
//  2   |   3
//      |
//--------------
//      |
//  0   |   1
//      |

Unfortunately this was very hard-coded for four quadrants. I wanted to see if I could write a reusable function that would return a normalized index float based on a variable amount of cells. Since we already have the st.x and st.y and floor functions, this should be fairly straightforward. This was my first attempt:

    
float getIndexGrid(vec2 _st, float numCells){
    float grid = floor(_st.y * numCells) * 1.0/numCells;
    grid += floor(_st.x * numCells) * 1.0/numCells;
    return grid * 0.5;
}

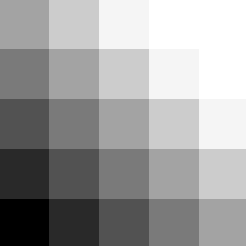
As you can see, while potentially useful in a differenent circumstance, this is not what we wanted. Instead of a left to right index, it's a gradient from the bottom left to the top right. To fix this logic error, we actually need one dimension, let's say y, to handle the big steps steps, like 0.1 in the case of 10 cells, and the x position to go up 0.01 steps to handle the 10 increments in between each 0.1.

    
float getIndexGrid(vec2 _st, float numCells){
    //y values, big steps.
    float grid = floor(_st.y * numCells) * 1.0/numCells;
    //x values close gap in between y values.
    grid += floor(_st.x * numCells) * 1.0/numCells * 1.0/numCells;
    return grid;
}

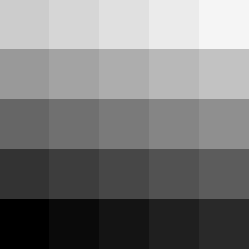
Now that we have this float value, we can use it to apply to any pattern we want. Here's the complete code applied to some rotating hemispheres.

float box(vec2 _st, vec2 _size){
    _size = vec2(0.5)-_size*0.5;
    vec2 uv = smoothstep(_size,_size+0.01,_st);
    uv *= smoothstep(_size,_size+0.01,vec2(1.0)-_st);
    return uv.x*uv.y;
}
    
vec2 rotate2D (vec2 _st, float _angle) {
    _st -= 0.5;
    _st =  mat2(cos(_angle),-sin(_angle),
                sin(_angle),cos(_angle)) * _st;
    _st += 0.5;
    return _st;
}

vec2 tile (vec2 _st, float _zoom) {
    _st *= _zoom;
    return fract(_st);
}

float getIndexGrid(vec2 _st, float numCells){
    //y values, big steps.
    float grid = floor(_st.y * numCells) * 1.0/numCells;
    //x values close gap in between y values.
    grid += floor(_st.x * numCells) * 1.0/numCells * 1.0/numCells;
    return grid;
}

float semiCircle(in vec2 _st, float radius){
    circle = 1.0 - smoothstep(radius, radius+0.001, length(_st));
    return box(_st, vec2(4.0, 1.0)) * circle;
}

void main (void) {
    vec2 st = gl_FragCoord.xy/u_resolution.xy;
    float numCells = 16.0;
    float index = getIndexGrid(st, numCells);
    st = tile(st,numCells);
    st = rotate2D(st,PI*(index)+(numCells*0.12*u_time));
	st -= 0.5;
    //color can use index to assign unique color to each cell. 
    vec3 color = vec3(1.0 - index, 0.7, 0.2+(index* 0.2));
    gl_FragColor = vec4(vec3(semiCircle(st, 0.5))*color,1.0);
}